
The
Material, Manufacturing and Computer Simulation of the Quenching Process of a
Japanese Blade

Abstract
Traditional methods of
preparing a kind of steel called tamahagane used for the Japanese sword by
tatara system and procedure of making the sword are briefly introduced with the
discussions from the viewpoint of metallurgy and thermo-mechanical processing.
Such traditional methods are also revealed to be consistent with the modern
science and technology. The quenching process applied to the final stage of the
procedure is focused to explain how the pattern of blade, the deformation and
residual stresses are induced by the computer simulation based on the theory of
metallo-thermo-mechanics relevant to the coupled fields among temperature, micro
structural change and stress/strain.
1.
Introduction
The
Japanese sword originally used as fighting weapon is now one of typical
traditional crafts with artistic characteristics, and so many monographs have
been published in English [1-6] as well as in Japanese. The sword is also
interesting from the viewpoint of modern science and technology [7-26] since the
way of manufacturing the sword is really consistent with the science as is same
as other surviving traditional products. Tawara, a professor of Japanese Sword
Research Laboratory, the
Very
few works on the sword were made, however, from mechanical engineering aspect.
Ishikawa[14-16] discussed the mechanism of cutting objects from theory of
cutting and the shape of the sword from dynamics, and stress/deformation
analysis after quenching by the finite element method was carried out by
Fujiwara and Hanabusa[17-18] and the present authors[19-26].
As is
well known, the Japanese sword is normally made of a traditional Japanese steel
made of iron sand, called tamahagane[27-31], and manufactured by a special way,
especially by folding the steel.In the first and second parts of the paper, the
process of preparing the steel and the way of making the sword are briefly
introduced.
One
of the most attractive and important stage of manufacturing the sword applied to
the end of the process before grinding and polishing is quenching, which induces
the characteristic deformation pattern of bending called sori, and the formation
of blade. The following parts treat some results of computer simulation of
interesting bent shape of the sword and pattern of the blade simulated by a
developed code 'HEARTS' [32-35].
The
code was accomplished based on the theory of metallo-thermo-mechanics[36-39]
relevant to describing the fundamental equations considering the coupling effect
among microstructural change, temperature and stress/strain, which have been
applied to the simulation of heat treatment processes considering phase
transformation including quenching of the sword[19-26]. After discussing an
paradoxical characteristics on the heat transfer coefficient between heated
steel covered by a kind of thermally insulated clay, called yakibatsuchi, and
water as the coolant, some results of simulation of a sword in the quenching
process are presented.
2.
PREPARATION OF TRADITIONAL JAPANESE STEEL
Almost all Japanese
swords with some exceptions are made of tamahagane
steel, or noble steel, specially prepared by the tatara system by use of iron
sand, but not by normal ore as seen in the old painting.

Fig.1
Old painting of tatara system.
Steels distributed in
The
steel was used not only for swords, but also for guns, cutting tools, nails for
construction of old temples and shrines, and other products necessary for
ordinary life.Around the period, the tatara system was replaced by the modern
western system except for providing the steel to sword smiths.
The
Iron and Steel Institute of Japan constructed an experimental system of Tatara
in [27-28]in Sugaya,
Due
to the lack of the steel for the sword, the
Iron
sand with 2-5\% content of iron mined from

Table 1 An
example of chemical composition of iron sand in virgin and enriched
states.
The
enriched iron sand is supplied alternatively to the furnace with charcoal by
hands. Figure 2 illustrates the cross
sectional view of the furnace under operation with some drainage mechanism
constructed to three meters under the ground. Only a difference of the system
from the classical one in Fig.1 is that
electric motors are used for intermittent air blowing instead of manpowered
bellows.

Fig.2
Cross sectional view of tatara furnace
Continuous burning is
operated for 70h under the direction of a murage, or chief foreman. The
temperature in the furnace is around 1200-1500 deg C lower than the melting
point of the steel, which follows that the reduction process of the partly
molten state is occurred between iron oxide Fe2O3 and silica SiO2 contained in
the clay of furnace. During the process, the initial thickness of 200-400mm of
the furnace is reduced to 50-100mm. After taking out the slag from the bottom of
the furnace followed by destroying the furnace, a block of blister steel called
kera in sponge state with dimension of 2.7m in length, 1m in width and 200-300mm
in thickness and with 2-2.5ton containing steel of 1.5-1.8ton is obtained (see
Fig.3), while necessary amount of iron
sand and charcoal are respectively 8 and 13tons. (It is amazing that the block
costs hundred thousand dollars, two hundred times much expensive of normal
steel!)

Fig.3
Kera, a block of blister steel.
Steel
produced on the both side of the block, where the enough deoxidization is
completed by air supplied from kirokan (special wooden pipes) is called
tamahagane, or noble steel, which is spelled as mother of metal in Japanese
character. Other parts of the block with different chemical composition in
Table 2 are also used for the sword
making.

Table 2.
Chemical composition of tamahagane, forged and core steels.
The
chemical compositions of the best part of steel are 1.0-1.4% C, 0.02-0.03% P,
0.006% S, and 0.003-0.004% Ti, being very rare of sulfur and phosphorus even
compared with industrial carbon steel (see Table
2).
The
steel is cooled by cold environment since the operation is carried out in
mid-winter followed by shattering, and distributed to about 300 professional and
registered sword smiths in
3.
MANUFACTURING OF JAPANESE SWORD
The
pieces of the steel with different carbon contents are heated in the carburizing
or decarburizing environment, termed jigane-oroshi. This process is made in the
furnace burnt by charcoal and ash of rice straws with the blowing air sent by
fuigo (blowers). Decarbonization occurs in the part closed to the blower, while
CO2 gas accelerates the sintering on the upper parts.
The successive process of
making a sword is illustrated in Fig.4.
The smith makes a flat plate with a handle termed as tekoita, on which the small
pieces of broken flat pieces are piled up covered by a special Japanese paper
dampened by water containing clay and rice straws to prevent oxidation on the
surface of steel by insulating air. It is known that SiO2 in the clay
contributes to increase the impurities including in the slag.
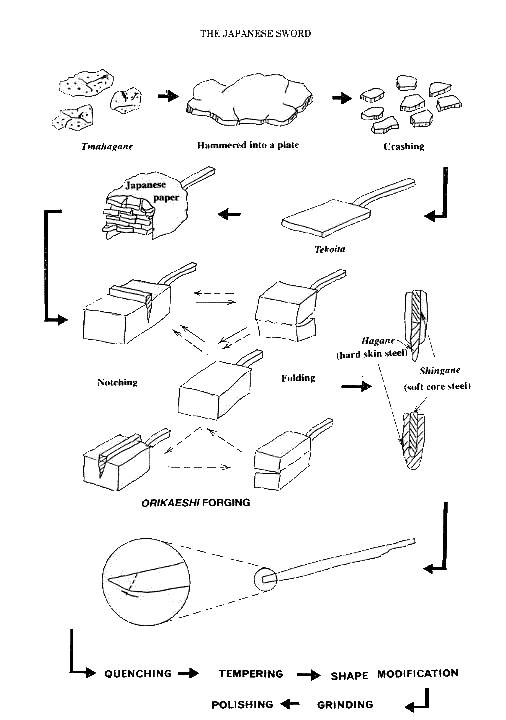
Fig.4
Process of manufacturing the Japanese sword.
Forging process is
followed to obtain a block, where about ten to fifteen rounds folding called
orikaeshi are repeated to get laminated materials with approximately 1,000
(=2**10) to 30,000 (=2**15) layers. The characteristic pattern of the laminated
layers depending on the way of smiths is visible on the surface of the sword,
some of which are depicted in Fig.5.

Fig.5
Laminated layers by orikaeshi forging.
Such
bonding of each layers during orikaesi process is enhanced by the mechanism of
so called mechanical alloying, for which so clean surface of the layers are
necessary. This is achieved by dispersing impurities such as oxides and so on
with sparks by hammering. The weight of the block decreases during the process
to approximately 700-100g in the final shape of the sword.
A bar
of shingane (core steel) with low carbon content is wrapped by kawagane or
hagane (skin steel) with high carbon for which the tamahagane steel is normally
used (see the cross sectional views in Fig.4). This process is called tsukurikomi. After
rough grinding by the smith himself, the sword is transferred to the final
process of yakiire (quenching), which is the main topics of numerical simulation
in the following sections.
Before quenching, a kind
of clay, yakiba-tsuchi, mixed by charcoal powder and so on is pasted on the
surface of the blade to control the heat transfer intensity to be discussed in
Sec.6 as presented in Fig.6.

Fig.6
Tsuchioki, pasting a kind of mixed clay on the blade.
Most
interesting situation is that the pasted clay is thick on the ridge while thin
on the blade part as illustrated in Fig.7
. Finally the quenching operation of the sword heated up to 800-850 degC into
water is carried out. (The temperature of heated sword and cooling water depends
on the school of smiths and the material property as well as the dimension of
the sword.)

Fig.7
Pasted pattern of the thickness of yakiba-tsuchi
During the quenching
process, a white hard part with martensite structure is induced near the blade,
while other shining part remains pearlite and ferrite structures. The border of
the parts is called hamon as seen in Fig.8.

Fig.8
Hamon, shape of border between quenched and unquenched parts.
Here,
wavy or zigzag pattern of the hamon is realized by cutting the clay by a
spatulas. A computer simulation how the hamon appears and how the stresses are
induced will be treated in the following sections.
4. SUMMARY OF
MEATALLO-THERMO-MECHANICS
In
such cases of quenching of the Japanese sword, and other machine parts in
general, incorporated with phase transformation, fields of metallic structure,
temperature and stress/deformation are coupled each other as schematically
illustrated in the diagram of Fig.9
[36-39].

Fig.9
Coupling effect among metallic structures, temperature and
stress/deformation.
Each
field is to be described by the coupled fundamental equations of kinetics of
phase transformation, heat conduction equation and constitutive equation
combined with kinematic relation and equation of motion, which are summarized in
separate page (see separate page of
5. FRAMEWORK
OF DEVELOPED CAE SYSTEM ''HEARTS''
Brief
introduction of the developed CAE system 'HEARTS' is presented in this section
to be used for the simulation of the quenching process of the Japanese
sword.
+++++ 5.1.
Finite Element Scheme and Method of Numerical Calculation ++++
Finite element scheme is
applied to the fundamental equations developed above, and a new version 2.0 of
'HEARTS' [35] approximately with 35,000 steps consisted of 250 subroutines in
several levels is coded by FORTRAN 77. For three dimensional problem as well as
two dimensional and axisymmetrical problems (plane stress and strain problems
including that of generalized plane strain for stress analysis), which were
available in the version 1.0. The 2-D and 3-D isoparametric elements with
variable-number-nodes are selected from an element library.
A
skyline scheme and modified or full Newton-Raphson method are employed to solve
these nonlinear equations in each time step. In order to treat unsteady heat
conduction equation depending on time, a numerical time integration scheme
'step-by-step time integration method' is introduced, while an incremental
method is used for deformation and stress analysis.
++++++++ 5.2.
Architecture of 'HEARTS' ++++++++
The
heat treatment simulation code ''HEARTS'' is utilized in the CAE circumstance as
illustrated in Fig.10 \ref{Architecture},
being combined with the solver, and pre/post processor such as PATRAN, I-DEAS,
or other popularly used processors, and the interface. The data necessary for
the simulation is generated by the pre-processor, is output in the form of
intermediate file. The data in the file is transferred into the data file for
control and initial-boundary conditions as well as the file for the element and
node data, while the material data file is constructed separately.

Fig.
10 System architecture of CAE system 'HEARTS'
The
solver of ''HEARTS'' is divided mainly into four parts corresponding to the
equations, and they can be connected by the user's requirement what kind of
solutions, coupled or uncoupled, to be solved. The output of the numerical
results calculated by the solver are transferred into the files for
post-treatment, list image and final results. The data for post-treatment is
again stored in the intermediate file through the interface to convert into the
final data for post-processor, and several kinds of illustration are available
by the user's requirement.
6.
IDENTIFICATION OF HEAT TRANSFER COEFFICIENT
Before quenching the
sword into water, the yakiba-tsuchi clay is pasted on the surface as shown in
Fig.6 to control the cooling condition of
the surface of the steel. Since the temperature distribution is to be calculated
in the body of the sword, it is necessary to identify the relative heat transfer
coefficient on the metal surface as the function of the thickness of the
clay.
Series of experiments
based on Japan Industrial Standard, JIS-K2242, were made to measure the cooling
curve of a cylinder made of silver coated by the clay with different thickness.
The reason of the usage of a silver is that the material is not undergone any
phase transformation during the heating and cooling process. A thermocouple is
mounted on the surface as shown in
Fig.11. The cylinder is heated up to 800 degC by a reflection type
electric furnace, and cooled in the water.

Fig.
11 A silver rod mounting a thermocouple
Obtained cooling curves
are demonstrated in Fig.12 as the
parameter of thickness of the pasted clay[43]. It is so interesting that the
curves for thick clay (t=0.7-0.8 and 0.75-0.9mm) show typical mode with moderate
cooling rate due to film boiling followed by severe cooling stage by nuclear
boiling, the shape of which are similar to the case without the clay. When the
thickness is small (t=0.1-0.15 and 0.2-0.3mm), on the other hand, no film
boiling stage is observed, which means that the cylinder is cooled severely from
the beginning. This is also confirmed by the observation of bubble nucleation by
video camera.

Fig.
12 Cooling curves on the surface of a silver rod depending on the thickness of
pasted clay.
Inverse calculation is
carried out by perturbation method to identify the heat transfer coefficient on
the surface of the cylinder. Results are represented in Fig.13. It is paradoxes to be noted from this
figure that the coefficient in the case with thin clay gives higher value than
without clay during 800-400 degC being most important temperature range for
quenching. This data will be employed as the boundary condition when solving the
coupled heat conduction equation.

Fig.
13 Temperature dependent heat transfer coefficient.
7. SIMULATED
RESULTS OF QUENCHING PROCESS
7.1. A Sword
Treated and the Condition of Simulation
The
shape and dimension of the sword treated here is illustrated in Fig.14, which is a model of a classical and famous
sword termed Bizen-Osafune.

Fig.
14. Shape and dimension of a sword treated.
Three
dimensional finite element mesh division of the sword is represented in Fig.15, where the division is made for a half part
in the width direction due to symmetry. Figures
15(a) and (b) respectively denote the whole region and the enlarged
part near kissaki(tip).

(a)Global
view.
(b)Near the
tip.
Fig.
15. Finit element mesh.
Total
number of the elements is 828, and that of the nodes is 1230. This model is
supposed to consist of two regions, (see Fig.16(a)), core steel with 0.2\% carbon content
and skin steel with 0.65%C to which different material data are applied. To
differentiate the relative heat transfer coefficient depending on the thickness
of the yakibatsuchi clay, the surface of the sword is divided into two parts
shown in Fig.16(b) with different value
indicated in Fig.13.

Fig.
16 Division of the sword for two materials with different carbon content (a) and
for two kinds of surface area with different heat transfer coefficient
(b).
The
sword is uniformly heated up to 850 degC, at which temperature the whole region
is changed into austenitic structure, and the sword is quenched into the water
of 40 degC.
7.2. Effect
of Pasted
To
know the effect of the thickness of clay on the induced hamon (border between
quenched and unquenched regions), simulation of quenching under several
different conditions were carried out. Red parts of Fig.17 show the volume fractions of martensite
after quenching for different way of pasted clay. When the sword is quenched by
pasting thick clay of 0.8mm, martensite hardly appear except for the part near
the blade (see Fig.17(a)), which follows
that very thin hamon occurs. However, almost whole region become martensite as
seen in Fig.(b) when thin clay with 0.1mm
thickness is pasted on the whole surface. If the clay is pasted thin on the
blade side, and thick on other part, on the other hand, ideal distribution of
martensite is obtained by the simulation with hardened blade by martensite and
with ductile main body by pearlite as is so realistic as the normal sword.
Hereafter, the simulation below is made with the pasted yakibatsuchi clay of the
final pattern.

Fig.
17 Martensite fraction corresponding to hamon, depending on the way of
thickness of
pasted
clay.
7.3.
Variation of Temperature, Metallic Structures, and Associated
Deformation
Figure
18 shows
the temperature distribution of the sword with successive time from the
beginning of the quenching, and the mode of deformation is also depicted in the
figure. The part of blade near the edge with thin thickness shrinks due to
thermal contraction by severe cooing, which leads to the bending to the downward
termed as gyaku-sori or reverse bending at t=1s as is shown in Fig.(b).

Fig.18
Successive deformation associated with temperature distribution.
When
martensitic transformation starts to occur in that part, however, normal bending
called sori to the upper direction is observed due to the volumetric dilatation
by martensite formation (see Fig.(c)).
Gyaku-sori again appears at t=3-4s, because of the pearlitic transformation in
the part of ridge. In the successive stage of cooling, hot ridge side shrinks
gradually because of thermal contraction, and finally, the normal bending can be
obtained.
Thus
simulated deformation gives the good agreement with the actual bending mode of
sori. Such mode of successive deformation due to martensitic and pearlitic
transformation is shown in Fig.19.

Fig.
19 Successive development of structures
7.4. Stress
Distribution and Residual Stresses
Stress distribution in
the longitudinal direction in the course of quenching is represented in Fig.20.

Fig.
20 Longitudinal stress distribution and residual stresses.
The
simulated residual stresses after complete cooling are compared with measured
data by X-ray diffraction technique on the lines along Hasaki (edge), Shinogi
(side ridge) and Mune (ridge)(see Fig.14)
as shown in Fig.21.

Fig.
21 Comparison of calculated residual stresses with experimental
data.
It is
also noted that the maximum stress near the top of the sword during quenching
reaches the fracture stress, which sometimes leads to cracking or breakage of
the sword during the operation.
8. CONCLUDING
REMARKS
Procedure of preparing
the traditional Japanese steel, tamahagane, followed by the method of making the
Japanese sword is summarized in the first part of the paper from the scientific
point of view. Theory of metallo-thermo-mechanics relevant to the simulation of
quenching processes and the brief introduction of the finite element computer
code 'HEARTS' are also stated.
As an
example of the application of the simulation of quenching processes, a Japanese
sword is focussed, and the change in temperature, metallic structure and
stress/deformation are calculated. The results reveal to represent such real
situations. The discussion from the viewpoints of metallurgy and mechanics are
carried out in each section of preparing Japanese steel and manufacturing the
sword, especially on the effect of pasted clay.
In
conclusion, the technology surviving for over thousand years is really
consistent with the modern science and technology.
Acknowledgements
The
author wish to express his hearty acknowledgement to Prof. K. Ishikawa, Kanazawa
Institute of Technology, Mr. J. Nozaki, Metal Museum, Mr. T. Suzuki, Nippon
Bijutsu Token Hozon Kyokai, for their providing instructive information on the
science of Japanese sword. Cooperation to develop the CAE system ''HEARTS'' and
identify the heat transfer coefficient are made respectively by Mr. K. Arimoto,
CRC Research Institute (now moved to SFTC Co.) and
***********
References ***********
1.
2.
3.
4.
5.
Museum of Fine Arts, Boston (ed.), Japanese Master Swordsmith ---The Gassan
Tradition, Museum of Fine Arts, Boston, (1989).
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
(in
Japanese), {\bf 38} (1993) 1.
18.
19.
20.
21.
22.
23.
24.
25.
26. T. Inoue, Materia (in Japanese),135 (1996) 81.
27.
Committee on Restoration Project of Tatara Steelmaking System, Restoration of
Tatara Steelmaking Process and the Blister Steel (in Japanese), ISIJ-Special
Report No. 9 (1970).
28.
29.
30.
K. Kubota, Coll. Int. Inst. CNRS, No.538 (1970) 577.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
H. Kanamori, E. Nakamura, S. Koyama and T. Inoue,J. Japan Soc. Heat
Treatment,36(1997